一、误差的基本概念:
1.误差的定义:
误差=测得值-真值;
因此,误差是一个值,数学上就是坐标轴上的一个点,是具有正负号的一个数值
2.误差的表示方法:
① 绝对误差:
绝对误差=测量值-真值(约定真值)
在检定工作中,常用高一等级准确度的标准作为真值而获得绝对误差。
如:用二等线纹玻璃尺校正全自动影像测量仪,二等线纹尺示值为300mm,校准全自动影像仪的示值为299.998mm,则全自动影像测量仪的测量误差为-0.002mm。
② 相对误差:
相对误差=绝对误差/真值X100%
相对误差没有单位,但有正负。
③ 引用误差:
引用误差=示值误差/测量范围上限(或指定值)X100%
引用误差是一种简化和实用方便的仪器仪表示值的相对误差。
3.误差的分类:
① 系统误差:在重复性条件下,对同一被测量进行无限多次测量所得结果的平均值与被测量的真值之差。
② 随机误差:测量结果与在重复性条件下,对同一被测量进行无限多次测量所得结果的平均值之差。
③ 粗大误差:超出在规定条件下预期的误差。

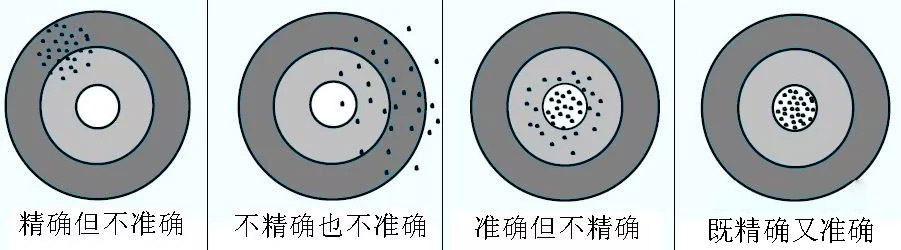
精度:
精度细分为:
准确度:系统误差对测量结果的影响。
精密度:随机误差对测量结果的影响。
精确度:系统误差和随机误差综合后对测量结果的影响。
精度是误差理论中的说法,与测量不确定度是不同的概念,在误差理论中,精度定量的特征可用目前的测量不确定度(对测量结果而言)和极限误差(对测量仪器仪表)来表示。对测量而言,精密度高的准确度不一定高,准确度高的精密度不一定高,但精确度高的准确度与精密度都高,精度是精确度的简称。目前,不提倡精度的说法。
一、三、测量不确定度
定义:表征合理地赋予被测量之值地分散性,与测量结果相联系地参数。
① 此参数可以是诸如标准差或其倍数,或说明了置信水准的区间的半宽度。
② 测量不确定度由多个分量组成。其中一些分量可用测量列结果的统计分布估算,并用实验标准差表征。另一些分量则可用基于经验或其他信息的假定概率分布估算,也可用标准偏差表征。
③ 测量结果应理解为被测量之值的最佳估计,而所有的不确定度分量均贡献给了分散性,包括那些由系统效应引起的(如,与修正值和参考测量标准有关的)分量。
由此可以看出,测量不确定度与误差,精度在定义上是不同的。因此,其概念上的差异也造成评价方法上的不同。
四、测量误差和测量不确定度的主要区别
1.定义上的区别:误差表示数轴上的一个点,不确定度表示数轴上的一个区间;
2.评价方法上的区别:误差按系统误差与随机误差评价,不确定度按A类B类评价;
3.概念上的区别:系统误差与随机误差是理想化的概念,不确定度只是使用估计值;
4.表示方法的区别:误差不能以±的形式出现,不确定度只能以±的形式出现;
5.合成方法的区别:误差以代数相加的方法合成,不确定度以方和根的方法合成;
6.测量结果的区别:误差可以直接修正测量结果,不确定度不能修正测量结果;误差按其定义,只和真值有关,不确定度和影响测量的因素有关;
7.得到方法的区别:误差是通过测量得到的,不确定度是通过评定得到的;
8.操作方法的区别:系统误差与随机误差难于操作,不确定评定易于操作;
误差与测量不确定度是相互关联的,就是说,测量误差也包含不确定度,反之,评定得到的不确定度也还是有误差。
|
序号 |
测量误差 |
测量不确定度 |
|
1 |
有正负的量值,其测量结果减去被测量的真值 |
无符号的参数,用标准差或标准差的倍数或置信之间的半宽表示 |
|
2 |
表明测量结果真值 |
表明测量值的分散性 |
|
3 |
客观存在不以人的认识程度而改变 |
与对测量,影响及测量过程的认识有关 |
|
4 |
由于真值未知,不能准确得到当用约定值代替真值,可得其估算值 |
可由依据实验,资料,经验等信息评定,从而可定量确定 |
|
5 |
按性质可分为随机误差和系统误差 |
不确定度分量评定时一般不分其性质,若需要可表述为:由随机效应引入的不确定度分量和由系统效应引入的不确定度分量 |
|
6 |
已知系统误差的估值时,可以对测量结果进行修正,得到修正后的测量结果 |
不能用不确定度对测量结果进行修正。在已修正的测量结果的不确定度中应考虑修正引入的不确定度 |
精度是按照误差的分类进行评价的,但在误差合成的方法上与测量不确定度是不同的,系统误差按照代数和合成,随机误差按方和根法合成,而系统误差与随机误差的合成则有按标准差合成的,有按极限误差合成的。因此,其合成的方法并不统一。



